Posts Tagged ‘Fermionen’
Wilhelm Reich, Physiker: 2. Orgonbiophysik, e. Mechanistische Äquivalente zum Orgonenergie-Akkumulator
16. Januar 2026The Journal of Orgonomy (Vol. 31, No. 2, Fall/Winter 1997)
21. August 20121928 führte George Gamow den „Tunneleffekt“ in die Physik ein. Gewöhnlich erklärt man ihn mit der Heisenbergschen Unbestimmtheitsrelation. Demnach sei es einem Teilchen möglich, ein an sich undurchdringliches Hindernis zu „durchtunneln“, weil es den Energieerhaltungssatz unterlaufen könne, solange es nach der Zeit-Energie-Unbestimmtheit „rechtzeitig“ die geliehene Energie zurückgibt. Ebenso könnte mit der Ort-Impuls-Unbestimmtheit argumentiert werden, die keine ruhenden, energielosen Objekte mit einer festen Lokalisation zuläßt, so daß man Quanten-Teilchen prinzipiell nicht „einsperren“ kann. Mit anderen Worten: es kann keine perfekte Abschirmung und damit keinen „leeren Raum“ geben.
Noch überzeugender wird das Argument, wenn die Unbestimmtheitsrelation unmittelbar auf den „leeren Raum“ angewendet wird. Beseitigt man alle Atome aus einem Behälter, um ein Vakuum zu erzeugen, bleibt die Wärmestrahlung zurück. Doch auch die läßt sich durch Abkühlung auf den absoluten Nullpunkt nicht abstellen, denn bei dem ist immer noch die „Nullpunktstrahlung“ vorhanden – und die würde auch „ohne Wände“ vorliegen. Nach der Zeit-Energie-Unbestimmtheit läßt sich nämlich Stärke und Änderungsrate eines Feldes nicht gleichzeitig festlegen. Da bei einem feldfreien Vakuum jedoch Feldstärke und Änderungsrate exakt bestimmt wären, ist ein solcher Zustand prinzipiell unmöglich. Quantenstatistisch ausgedrückt bedeutet dies, daß man die Wahrscheinlichkeitswelle niemals ganz beseitigen kann – ein Rest von Wahrscheinlichkeit bleibt immer. Deshalb kann es in der Quantenmechanik weder eine perfekte „Isolation“ noch ein Vakuum geben; stets müssen in jedem denkbaren Bereich des leeren Raumes „Vakuumfluktuationen“ auftreten.
Merkwürdigerweise begann die neue „Äther-Physik“, als man die Quantenmechanik mit der Relativitätstheorie verband. Den ersten Schritt in diese Richtung unternahm 1928 Paul Dirac, als er die Quantenwellenfunktion für Elektronen relativistisch verbesserte. Diese modifizierte Gleichung ergab auch Lösungen für „negative Energie“. Demnach könnte ein Elektron auf ein Energieniveau springen, das unterhalb seiner Nullenergie liegt. Das Atom wäre also wieder genauso instabil, wie vor Bohrs Atommodell. Um diese Katastrophe zu verhindern, postulierte Dirac Elektronen mit negativer Energie, die alle denkbaren negativen Energieniveaus und damit den gesamten Raum auffüllen. Dirac selbst sprach ausdrücklich vom „neuen Äther“. Das Neue an diesem Äther war, daß er aufgrund des auf ihn angewendeten Unbestimmtheitsprinzips, das die Zuordnung einer bestimmten Geschwindigkeit verhindert, im Gegensatz zum klassischen stationären Äther nicht im Widerspruch zur Speziellen Relativitätstheorie stand.
Ein energiereiches Photon kann ein „negatives Elektron“ aus diesem „Dirac-See“ heben, indem es (z.B. mit einem anderen als „Katalysator“ dienenden Elektron zusammenstößt und dabei) sozusagen ein „Loch“ in das Vakuum schlägt. Das Loch entspricht einem damals noch hypothetischen „Positron“ (das dann 1932 tatsächlich von Anderson entdeckt wurde). Wird dieses Loch vom Elektron wieder aufgefüllt, indem sich Elektron und Positron vereinigen, entsteht ein identisches Photon.
In der „Quantenfeldtheorie“ (Quantenmechanik, die sich mit Wechselwirkungen befaßt) wurde wohl später der unbeobachtbare Dirac-See, in den man „Löcher“ schlagen konnte, fallengelassen (zumal immer mehr „Elementarteilchen“ entdeckt wurden, für die jeweils eigene „Seen“ hätten postuliert werden müssen), doch das Vakuum ist in der Vorstellung der Quantenfeldtheorie nach wie vor ein brodelnder See, bzw. ein „Gas“ aus „virtuellen Teilchen“, die durch die beschriebene Paarbildung „aus dem Nichts“ auftauchen und wieder vergehen.
1958 konnte M.J. Sparnaay erste Anzeichen einer meßbare Wirkung dieser virtuellen Teilchen nachweisen, als er einen 1948 von Hendrick Casimir postulierten Quanten-Effekt überprüfte. Zwei ungeladene Metallplatten, die, durch einen sehr kleinen Abstand getrennt, sich parallel gegenüberstehen, werden im vollkommenen Vakuum bis zum absoluten Nullpunkt abgekühlt (was beides natürlich nur annähernd erreichbar ist). Das mit den virtuellen Teilchen assoziierte elektromagnetische Spektrum (oder anders ausgedrückt die erwähnte Nullpunktstrahlung) wird zwischen den Metallplatten eingeschränkt, wodurch sich die beiden Platten anziehen, bzw. gegeneinander gepreßt werden. Die Kraft, mit der dies geschieht, ist dafür, daß sie „aus dem Nichts kommt“, beachtlich.
Der amerikanische Physiker H.E. Puthoff vom Institute for Advanced Studies at Austin führt nach einer kurzen Beschreibung des Quantenvakuums und der diversen Effekte, die ihm zuzuschreiben sind, aus:
So stellen wir fest, daß die Quantenelektrodynamik, die in der Relativitätstheorie wurzelt, welche den Äther verbannt hatte, gewisserweise den Kreis geschlossen hat, um uns mit dem Modell eines energetischen Vakuums auszustatten, das wieder ein vollkommen ausgefüllter Raum statt eine Leere ist.
Er diskutiert sogar die Möglichkeit diesen kosmischen Energie-Ozean mit Hilfe des Casimir-Effekts anzuzapfen („The Energetic Vacuum: Implications for Energy Research“, Speculations in Science and Technology, 13,3:247-257, 1990) – etwas was Reich mit anderen Mitteln schon vor einem halben Jahrhundert in der Praxis gelungen ist.
Anläßlich der „Demonstration of the Casimir Force in the 0.6 to 6 µm Range“ (1997) von Steve K. Lamoreaux setzt sich das Journal of Orgonomy mit der Beziehung zwischen dem Casimir-Effekt und Reichs Entdeckung der Orgonenergie auseinander: „The Orgone Energy Continuum“ (S. 258-262). Siehe auch Malcom W. Browne: „Ether Re-emerges as the Je Ne Sais Quoi of Physics“ (Journal of Orgonomy, 32,2, Fall/Winter 1998, S. 259-263).
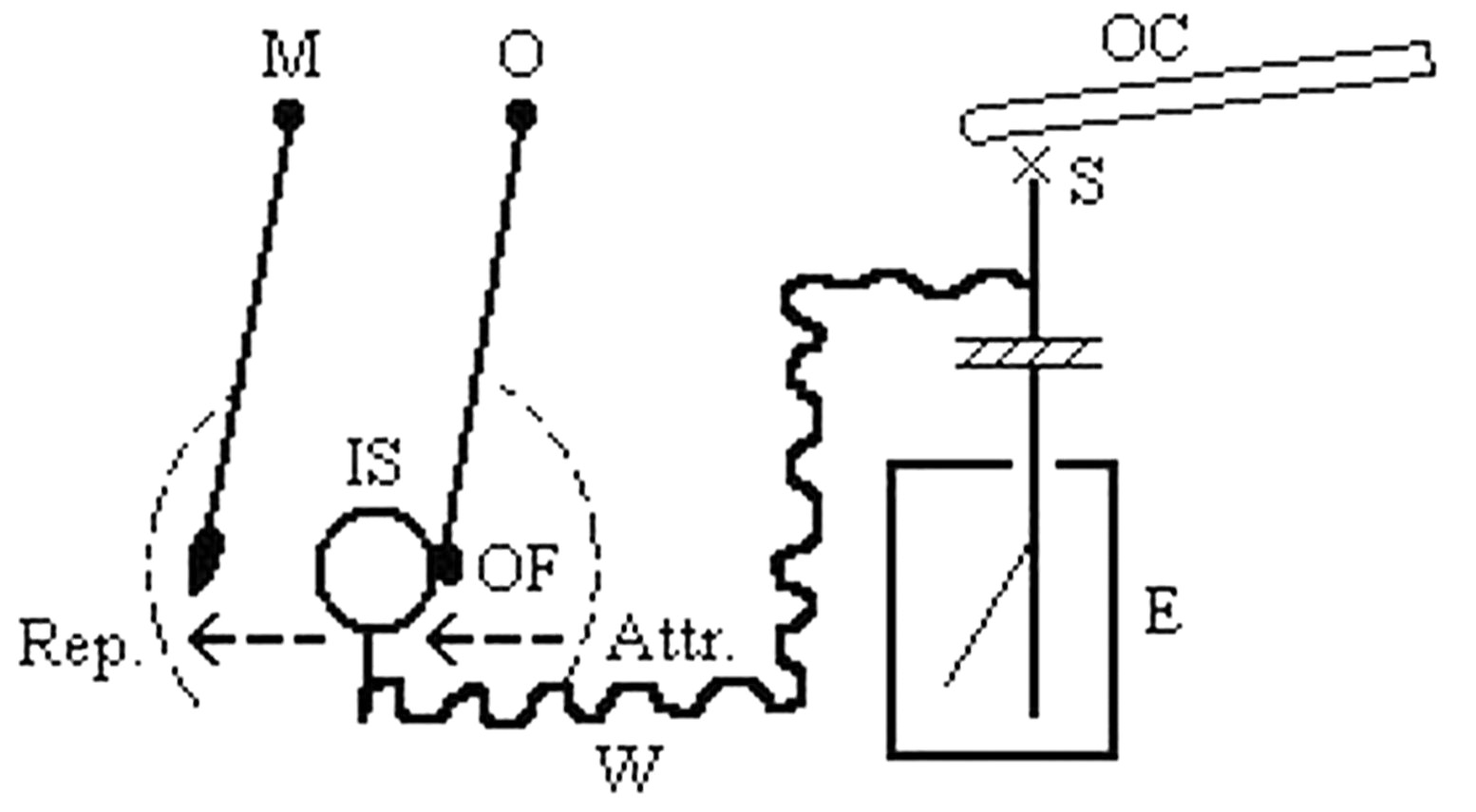
Das besondere am Casimir-Effekt ist, daß Bosonen (beispielsweise Photonen) zu einer anziehenden Casimir-Kraft, Fermionen (beispielsweise Elektronen) jedoch zu einer abstoßenden Casimir-Kraft führen. Das entspricht, dem Journal of Orgonomy zufolge, der gleichzeitig anziehenden und abstoßenden orgonotischen Kraft von Metall. Man denke etwa an den Orgonenergie-Akkumulator mit seinen abwechselnden Schichten aus „organischem“ und metallischem Material. Das nichtmetallische Material absorbiert und hält die atmosphärische Orgonenergie, während das Metall das Orgon zwar ebenfalls anzieht, aber es sofort wieder abstößt. Dies generiert im Orgonenergie-Akkumulator eine höhere Orgonenergie-Konzentration.
Mit dem Casimir-Effekt habe ich mich bereits an anderer Stelle beschäftigt.