Zeit messen wir mit Uhren, d.h. mit Schwingungen, etwa die eines Pendels. Setzen sich diese Schwingungen im Raum fort, haben wir Wellen vor uns. Wellen können wir mit der Kreisel-Welle und Schwingungen mit der Pulsation (Hin und Herschwingen) gleichsetzen. Siehe dazu S. 131 von Das ORANUR-Experiment II (Contact with Space):

Das orgonotische System, das im Solar plexus zentriert ist, pulsiert „auf der Stelle“ und ist der Taktgeber des Organismus, während das senso-motorische energetische Orgonom mit seinen weitreichenden Sinnesorganen und der von ihm kontrollierten Motorik weit in den Raum greift.
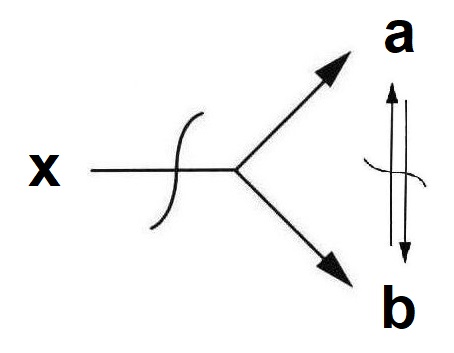
Im Schlaf, wenn unser Körper weitgehend paralysiert ist, gehen wir ganz und gar im Vegetativen Nervensystem auf, das die Struktur gewordene Funktion Pulsation ist: Kontraktion = Sympathikus, Expansion = Parasympathikus. In den Träumen dreht sich alles um die Vergangenheit und wir verarbeiten und „strukturieren“ das Vergangene. Erst im Schlaf wird das wirklich abgespeichert, was wir den Tag über gelernt haben. Auf Zellebene, in der Epigenetik, laufen ähnliche Prozesse ab. Orgonometrisch drückt man das mit folgender heterogenen Funktionsgleichung aus, die uns auf den Bereich der koexistierenden Wirkung verweist:

Am Tag heben wir umgekehrt Strukturen („Getrenntheit“) auf, etwa indem wir von beispielsweise von Hamburg nach Bremen gehen: das Pendel wird zur Welle! Man betrachte jedes beliebige Tier, wie es sich fortbewegt: es zeichnet eine Version der Kreiselwelle in den Raum. Im obigen Beispiel kommt es durch unsere Bewegung zu einem „Zusammentreffen von Hamburg und Bremen“ und wir stellen dementsprechend so etwas wie „Synchronizität“ her. Obzwar Bewegung („L/t“) das funktionelle Gegenteil von koexistierender Wirkung („Synchronizität“) ist, die durch die beiden Gleichungen „t –> L“ und „L –> t“ beschrieben wird, verweist auch dies auf eine heterogene Funktionsgleichung:

Die Frage ist, ob es im Bereich der koexistierenden Bewegung umgekehrt auch Verweise auf die relative Bewegung gibt. Schauen wir uns zunächst die entsprechende Entwicklungsgleichung an:
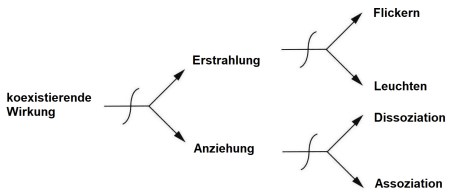
Im Traum erleben wir unmittelbar was orgonotische Erstrahlung (t –> L) ist und bekommen ein Gefühl dafür, was generell das Phänomen „Bewußtsein“ ausmacht. Der Ausdruck: „Ihm geht ein Licht auf“, wenn man beginnt etwas zu verstehen, bringt das gut zum Ausdruck. Auch Begriffe wie „Erleuchtung“ oder „Einsicht“ weisen in die gleiche Richtung. In der Natur beobachten wir die Erstrahlung beispielsweise in der Kreiselwelle mit ihrem Wechsel von kurzen, „materieartigen“ Pulsen zu langgestreckten, „feldartigen“ „Schwüngen“ und umgekehrt. Die Pulse entsprechen dem interminierenden Flickern („Schein“) der Erstrahlung, die „Schwünge“ an das beständige Leuchten („Sein“) der Erstrahlung. Siehe dazu S. 64 und S. 66 von Das ORANUR-Experiment II). Dabei sind bei aller funktioneller Entsprechung Kreiselwelle („L –> t“) und Erstrahlung („t –> L“) nicht dasselbe, wie ja auch anhand der beiden gegensätzlichen heterogenen Funktionsgleichungen deutlich wird.
Der Inhalt des Traumes und des Bewußtseins allgemein wird durch die Funktion Anziehung (L –> t) beschrieben, die sich in die beiden Variationen „Assoziieren“ (Verbinden) und „Dissoziieren“ (Trennen) aufspaltet. Man denke etwa an die Filmkunst, insbesondere surrealistische Filme, wo einerseits die separatesten Dinge so aneinandergereiht werden, daß sich durch deren Abfolge „assoziativ“ mehr oder weniger „sinnvolle“ Zusammenhänge ergeben (schwarze Haare – schwarzer Asphalt – abgründig „schwarze“ Gedanken – freier Fall) bzw. der Zuschauer durch all die Wirrheit selbst in einen dissoziativen Zustand versetzt wird und es zu Desrealisationserleben kommt. Religion und sogenannte „Spiritualität“ (man denke nur an Nahtodeserfahrungen) handeln wirklich von nichts anderem, d.h. von Assoziieren und Dissoziieren.
Assoziieren und Dissoziieren: die Nähe zu Kontraktion und Expansion fällt sofort ins Auge, aber auch hier handelt es sich nicht um dasselbe, allein schon weil Pulsation mit „t –> L“ („Gedächtnis“) beschrieben wird, während Anziehung (L –> t) das funktionelle Gegenteil von Gedächtnis ist.