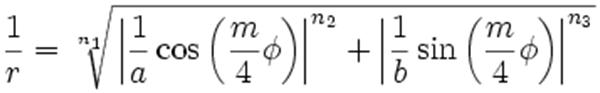Posts Tagged ‘Gleichungen’
David Holbrook, M.D.: Die Grenzen und potentiellen Gefahren des Entweder-oder-Denkens und seine Beziehung zu „Funktionalismus“ und „Orgonometrie“
25. September 2025Humana conditio ex orgonomico prospectu: Stichwort „Der medizinische Orgonom” und folgende
10. Januar 2025Orgonometrie (Teil 3): Kapitel 1
1. Januar 2019nachrichtenbrief69
13. September 2017
Die kosmische Überlagerung und die Weltformel
6. Februar 2015Reichs Buch Die kosmische Überlagerung (die deutsche Übersetzung des 1951 erschienenen Buches Cosmic Superimposition) ist 1997 im Verlag Zweitausenundeins erschienen. Leider ist die Edition schon seit langem vergriffen, aber beispielsweise über amazon kann man antiquarische Exemplare erwerben.
In diesem Werk hat Reich versucht, die Formen der Natur über die „Kreiselwelle“ zu beschreiben, die spezifische Bewegungsform der Orgonenergie. Mathematisch betrachtet ist sie eine „verlängerte Zykloide“. Mechanisch entspricht sie der Bahn eines Punktes außerhalb eines abrollenden Kreises.
Johan Gielis (Universität Nijmegen) hat eine mathematische Formel entwickelt, die der Beschreibung eines Kreises gleicht, modifiziert durch einen Parameter, mit dem sich das Seitenverhältnis des geometrischen Objekts steuern läßt, und einen zweiten, der die Symmetrie verändert. Gielis glaubt, daß diese Formel die Formen in der Natur erklären kann.
Nicht geklärt sei, welche Art von physikalischer Dynamik hinter der Formel steckt. Allerdings habe die mathematische Beschreibung einer biologischen Struktur schon oft Hinweise auf den zugrundeliegenden Mechanismus offenbart.
Zu Gielis „Superformel“ siehe hier, wo diverse Abbildungen zeigen, daß wirklich alle Formen in der Natur von der Forml beschrieben werden: von Blüten, Insekten, Mikroorganismen, Spiralen, Kreiselwellen bis hin zu Rechtecken.
r: Abstand vom Mittelpunkt
Φ: Winkel zur x-Achse
m: Symmetrie
n1, n2, n3: Form
a, b: Ausdehnung (Halbachsen)